이산수학/집합과 논리 - 논리

부정 ~p

• 명제 p에 대하여 p의 진릿값을 반대로 갖는 명제를 위와 같이 표기하며 p가 아니다 또는 not p라고 읽는다.
  • p가 참인 명제일 경우 ~p는 거짓
  • p가 거짓인 명제일 경우 ~p는 참

논리곱(and) : p ∧ q

• 명제 p,q에 대하여 p와 q가 모두 참일 경우에만 참이고 그렇지 않을 경우 거짓이 되는 명제

논리합(or) : p ∨ q

• 명제 p,q에 대하여 p와 q가 모두 거짓일 경우에만 거짓이고 그렇지 않을 경우 참이 되는 명제

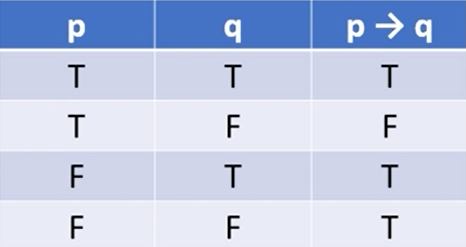
조건 명제 p → q

• 명제 p,q에 대하여 p가 가정이고 q가 결론이 되는 명제이다.
• 이 때 p이면 q이다. 또는 if p, then q 등으로 읽는다.
  • 주의
    • 조건명제 p → q의 진릿값은 p가 거짓일 경우 항상 참이고 p가 참일 경우 q의 진릿값과 일치한다.

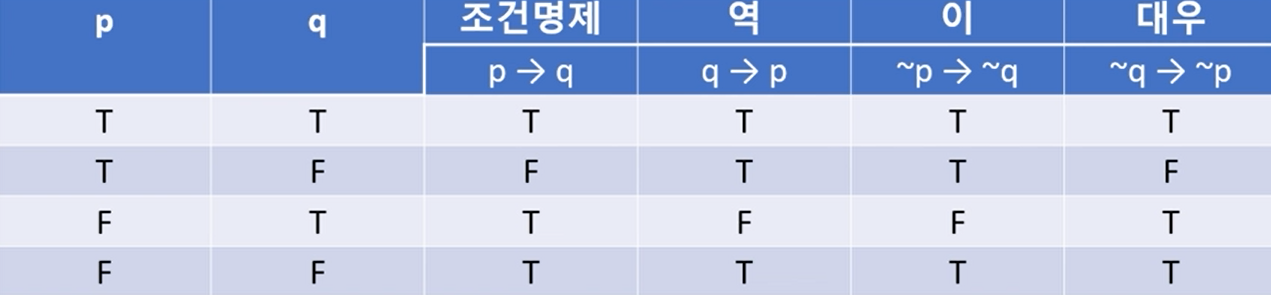
역

• 조건 명제 p → q에 대하여 가정과 결론이 바뀐 q → p를 p → q의 역이라 부른다.

이

• 조건 명제 p → q에 대하여 가정과 결론을 각각 부정한 ~p → ~q를 p → q의 이라 부른다.

대우

• 조건 명제 p → q에 대하여 가정과 결론이 바뀐 동시에 부정한 ~q → ~p를 p → q의 대우라 부른다.

명제함수와 한정자(quantifier)

명제함수 P(x)

• 변수 x를 포함하여 진릿값을 판별할 수 있는 문장이나 수식.
  • 예) P(x)가 x + 1 = 0 이라는 명제 함수라고 하자. 그러면 x의 값에 따라 P(x)의 진릿값을 판별할 수 있다.
    • x가 1일 경우 P(1)은 1 + 1 = 0 이라는 명제가 되고 이는 거짓인 명제이다.
    • x가 -1일 경우 P(-1)은 -1 + 1 = 0 이라는 명제가 되고 이는 참인 명제이다.

전체한정자 ∀

• 모든 값에 대하여 라는 말을 쓸 때 ∀라는 수학기호를 쓰며 영어로 for every라고 읽는다.
• ∀xP(x)또는 for every x, P(x)라는 명제는 논의의 대상이 되는 모든 x에 대하여 참일 경우 참인 명제이다.

존재한정자 ∃

• 어떤 값이 존재하여 라는 말을 쓸 때 ∃ 라는 수학기호를 쓰며 영어로 there exists라고 읽는다.
• ∃xP(x) 또는 there exists x, P(x)라는 명제는 P(x)가 참이 되는 x가 하나라도 있을 경우 참이되는 명제이다.