이산수학/집합과 논리 - 집합
집합
- 여러 원소들(element)의 모임으로 중복된 원소를 가지지 않음.
- 집합의 표기법
- 원소나열법 : 집합에 속하는 원소들을 일일이 나열하는 방법
- ex) a = {1, 2, 3, 4, 5}
- 조건제시법 : 집합에 포함되는 원소들의 성질을 조건식으로 제시하는 방법
-
ex) a = {x 0 < x <= 10}
-
- 원소나열법 : 집합에 속하는 원소들을 일일이 나열하는 방법
벤 다이어그램
- 집합 사이의 관계를 표시하기 위해 도형으로 표기한 것
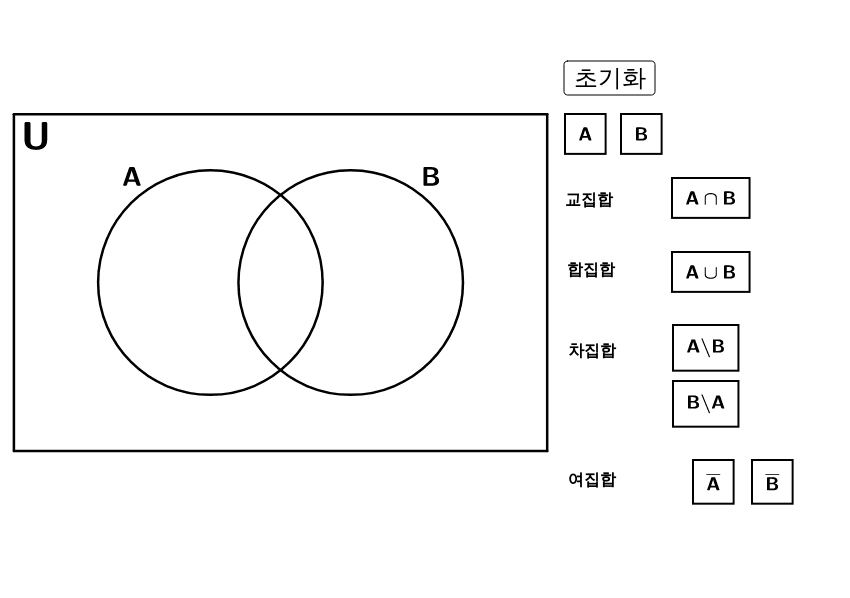
- 위의 그림에서 U,A,B는 각각 집합을 표현한 것이다.
유한집합 / 무한집합
- 집합 A에 속하는 원소의 개수를
|A|로 표현하며, 원소가 유한개인 집합을 유한집합, 원소가 무한개인 집합을 무한집합이라고 한다.
집합의 종류
- 전체 집합
- 논의 대상이 되는 원소 전체를 포함하는 집합으로 보통 알파벳
U로 표기한다.
- 논의 대상이 되는 원소 전체를 포함하는 집합으로 보통 알파벳
- 공집합
- 원소를 하나도 가지지 않는 집합으로
Ø또는{}로 표기
- 원소를 하나도 가지지 않는 집합으로
- 예시
- 자연수 전체의 집합 U와 자연수 중 3의 배수의 집합 A, 자연수 중 2의 배수의 집합 B가 있다고 하자.
그럼 아래와 같은 벤 다이어그램으로 표현된다.
- 자연수 전체의 집합 U와 자연수 중 3의 배수의 집합 A, 자연수 중 2의 배수의 집합 B가 있다고 하자.
집합의 포함관계
- 집합 A, B에 속하는 원소가 모두 동일할 때, 두 집합은 서로 같다고 하며 기호로
A = B로 표시한다. - 부분집합 :
A ⊆ B- 집합 A의 모든 원소가 집합 B에 포함될 때 A는 B의 부분집합이라 하고 위와 같은 기호로 표시한다.
- 진부분집합 :
A ⊂ B- 집합 A가 집합 B의 부분집합이지만
A = B는 아닐 경우 A는 B의 진부분집합이라 한다.
- 집합 A가 집합 B의 부분집합이지만
원소와 집합의 포함 관계
- 원소 a가 집합 A에 포함될 때
a ∈ A로 표시하고 a는 A의 원소다 라고 읽는다. - 원소 a가 집합 A에 포함되지 않을 때
a ∉ A로 표시하고 a는 A의 원소가 아니다 라고 읽는다.
합집합 : A∪B
- A의 원소들과 B의 원소들을 모두 모은 집합을 A와 B의 합집합이라 하며 위와 같이 표기한다.
- 아래의 벤 다이어그램에서 아래에 색칠된 부분을 뜻한다.
교집합 : A ∩ B
- A에 속하는 원소임과 동시에 B에도 속하는 원소들의 집합을 교집합이라 하며 위와 같이 표기한다.
- 아래의 벤 다이어그램에서 아래에 색칠된 부분을 뜻함.
서로소
- 집합 A와 B에 공통으로 속한 원소가 하나도 없을 경우 서로소라 부른다.
차집합 : A - B
- A의 원소 중에서 B에 속하지 않는 원소만으로 이루어진 집합을
A - B라 하며A - (A ∩ B)와 같다.
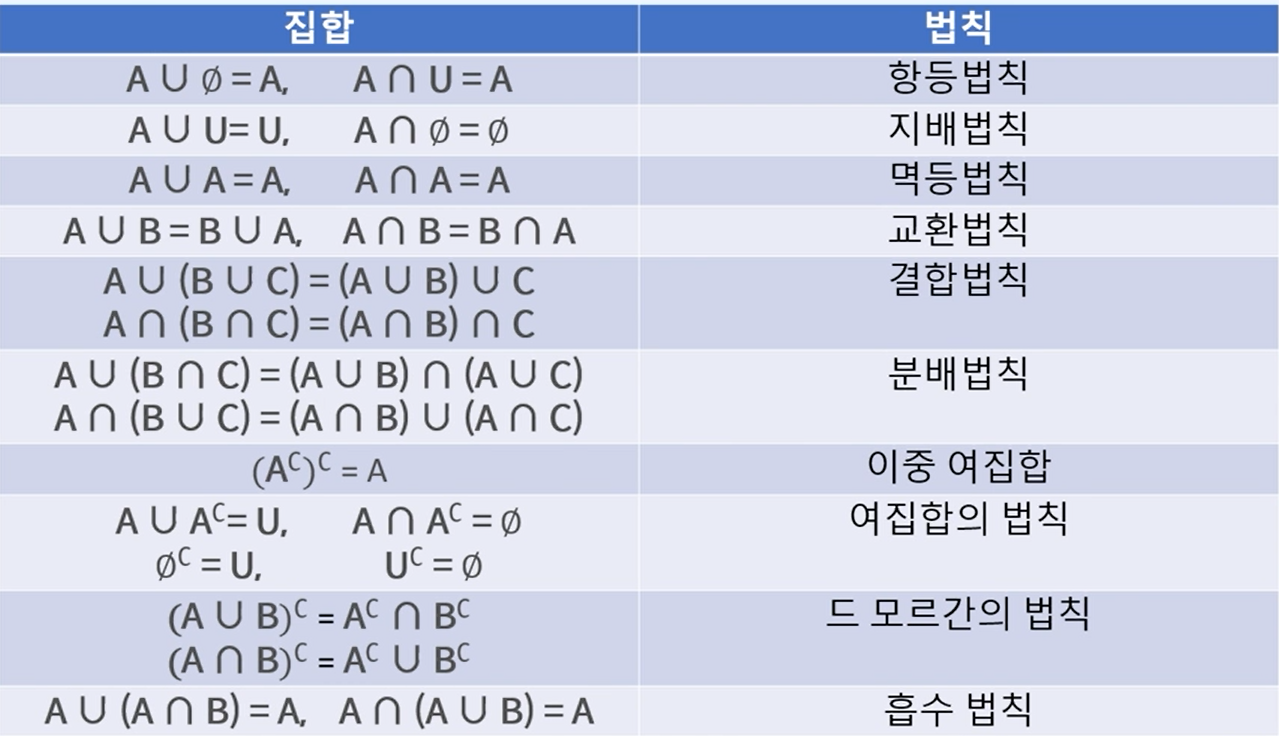
여집합 : AC
- 집합 A에 속하지 않지만 전체집합 U에 속하는 원소들의 집합을 A의 여집합이라 하며 위와 같이 표기한다.

Leave a comment